Precies of nauwkeurig? Je instrumenten moeten het allebei zijn!
op

Bij het schrijven van technische artikelen lopen we vaak het risico dat we taalkundige nauwkeurigheid over het hoofd zien, en dit wordt nog duidelijker in strenge vakgebieden - zoals metrologie - waar elke term een zeer specifiek gebruik heeft en, over het algemeen, ongepaste terminologie niet goed wordt getolereerd.
Metingen
Een meting is per definitie een numerieke relatie die het resultaat is van de vergelijking van een bepaalde grootheid met een andere, homogene grootheid met een bekende waarde, die als referentie wordt beschouwd.
Ongeacht de meeteenheid kunnen deze meting, vergelijking en de daaruit voortvloeiende berekeningen niet foutloos zijn. Fouten zijn inherent aan metingen; ze kunnen worden verminderd, maar niet geëlimineerd. Wat we kunnen doen - ermee leven - in de technische en wetenschappelijke sfeer, is de omvang ervan kwantificeren en het beschouwen binnen de context van het totale meetproces.
In het algemeen geldt voor T&M dat kwaliteit loont: De beste en duurste meetinstrumenten kunnen de marge van een meetfout verkleinen en zo de kwaliteit van ons werk verbeteren. Hier hangt echter een prijskaartje aan; technici en ingenieurs moeten voor de aanschaf de kwaliteit van het instrument dat ze gaan kopen evalueren, waarbij ze misschien een afweging moeten maken tussen prijs en prestatie.
Termen als precisie, nauwkeurigheid, herhaalbaarheid, stabiliteit op lange termijn, gevoeligheid, resolutie, gereedheid en volledige-schaalwaarde zijn algemeen gangbaar geworden en kunnen helpen bij het maken van een keuze uit de overvloed aan apparaten die op de plank verkrijgbaar zijn.
In dit scenario zijn twee daarvan echter de meest illustere slachtoffers: precisie en nauwkeurigheid, die vaak door elkaar en onjuist worden gebruikt (wat niet noodzakelijkerwijs veel kwaad kan).
Een eerste definitie
Wat betekenen nauwkeurigheid en precisie eigenlijk in de meettechniek? Laten we beginnen met twee beknopte definities:
- Nauwkeurigheid: Een instrument wordt gedefinieerd als nauwkeurig als het in staat is om consistent metingen te leveren die zo dicht mogelijk bij een referentiewaarde of werkelijke waarde liggen.
- Precisie: Een instrument wordt gedefinieerd als precies als het in staat is metingen te leveren die zo consistent mogelijk correleren met de gemiddelde waarde van de metingen.
Nu we ze kort hebben gedefinieerd, moeten we iets belangrijks opmerken: met slechts één beschikbare aflezing kunnen we de nauwkeurigheid van een instrument definiëren (zij het bij benadering), maar niet de precisie, waarvoor we een gemiddelde waarde of eventueel een getal nodig hebben, zodat de berekeningen statistisch significant zijn en een betrouwbaar resultaat opleveren.
Voordat we hier dieper op ingaan, is het echter de moeite waard om eerst een paar woorden te wijden aan het definiëren van het begrip 'fout'.
Meetfouten
In een enkele meting kan de fout gedefinieerd worden als het verschil tussen de gemeten waarde X en de werkelijke waarde θ (of de referentie waarde, als we aannemen dat die waar is) van de hoeveelheid in kwestie. In dit geval wordt het meestal gedefinieerd als een absolute fout, of η = X - θθ.
De absolute foutwaarde is slechts een deel van de informatie, omdat het ons geen enkele aanwijzing geeft over de verhouding van deze fout ten opzichte van de hoeveelheid die we vergelijken. Daarom wordt de grootte van een fout vaak uitgedrukt als de verhouding van de absolute fout η tot de ware waarde θ, dus gedefinieerd als relatieve fout, of ε = η / θ.
Deze fout kan alleen berekend worden als de referentiewaarde, θ, bekend is. De waarde van ε wordt meestal uitgedrukt als percentage, door deze met 100 te vermenigvuldigen. Daarom wordt de procentuele fout meestal aangegeven voor elk afzonderlijk bereik van een meetinstrument.
Soorten fouten
Er kunnen veel oorzaken zijn voor fouten in een experimentele meting, waaronder procedurele (bijvoorbeeld bedieningsfouten). Met name bij analoge meetinstrumenten worden bedieningsfouten significanter, zoals beschreven in het tekstkader Analoog vs. Digitaal uitlezen: De resolutie is van belang!
Hier gaan we er echter van uit dat er geen bedieningsfouten zijn en dat eventuele fouten voornamelijk afhangen van willekeurige factoren en van de eigenschappen van het apparaat.
We kunnen deze fouten onderverdelen in twee macrocategorieën:
- Systematische fouten, die de metingen constant in één richting sturen. Dit type fout kan in sommige gevallen verminderd of geëlimineerd worden. Het beïnvloedt vooral de nauwkeurigheid van een instrument.
- Willekeurige fouten, die bepaald worden door de technische eigenschappen van het instrument, de kwaliteit van het ontwerp en de gebruikte componenten, en door alle onvoorspelbare en/of oncontroleerbare gebeurtenissen die zich tijdens de meting kunnen voordoen. Dit type fout, dat voornamelijk de nauwkeurigheid van een instrument beïnvloedt, kan niet worden geëlimineerd, maar kan op zijn minst worden geschat door de meting meerdere keren te herhalen en de resulterende statistieken te analyseren.
In een elektronisch meetinstrument kunnen systematische fouten bijvoorbeeld worden veroorzaakt door langetermijnvariaties in de eigenschappen van de gebruikte componenten (derating) of door kortetermijnvariaties, zoals een bedrijfstemperatuur die buiten het bereik van het apparaat ligt. Op apparatuur van hogere kwaliteit zijn meestal een of meer kalibratie-opties voorzien om de omvang van deze fouten te beperken, via hardware of software.
Willekeurige fouten kunnen daarentegen worden veroorzaakt door elektromagnetische interferentie (EMI) die door de meetsnoeren wordt geleid, of door de inherente instabiliteit of slechte kwaliteit van de signaalconditionering en/of het sampling front-end. Ze kunnen gedeeltelijk worden verminderd door afscherming, maar er kan niets worden gedaan om een ontwerp te corrigeren dat fundamenteel tekortschiet of slecht functioneert.
Analoge vs. digitale uitlezing: Resolutie is belangrijk!
De resolutie van een meetinstrument is de kleinste variatie in de gemeten grootheid die het apparaat betrouwbaar kan detecteren en weergeven.
In het voorbeeld in de afbeelding zijn een vintage Cassinelli & C. analoge milliampèremeter (circa 1960) en een Siglent SDM3055 digitale multimeter van de laatste generatie (2024) in serie aangesloten op een stroomgenerator die is ingesteld op 30 mA. De bovenste afbeelding toont de 0...50 mA schaal van het oude instrument - waarvan de nauwkeurigheid absoluut opmerkelijk is, hoewel het meer dan 60 jaar oud is! - met 1 mA grote verdelingen en 0,5 mA kleine verdelingen. De resolutie van dit instrument is dus 0,5 mA (500 µA).

Hier is het kritieke aspect het beoordelen (optisch richten) van de positie van de naald in de gebieden tussen de verdelingen, met evaluaties die onvermijdelijk persoonlijk, arbitrair en sterk variabel zijn van gebruiker tot gebruiker.
Met het digitale instrument geeft het display een uitlezing van 29.690 mA op vijf cijfers - waarbij het minst significante cijfer staat voor de kleinste grootheid die het instrument kan meten en weergeven, d.w.z. 0,001 ma (1 µA). Het spreekt voor zich dat de resolutie geen conclusies toelaat over nauwkeurigheid of precisie!
Een eerste praktijkvoorbeeld
Stel dat we 4 multimeters in ons laboratorium hebben staan en we willen hun betrouwbaarheid controleren. In het laboratorium hebben we een hoogwaardige referentie-stroomgenerator beschikbaar en we stellen deze in voor een voorafgaande go-no-go test op een van deze instrumenten.
Om de test uit te voeren, stellen we de stroomgenerator in op 2,000 A, en we beschouwen deze waarde als de werkelijke waarde, referentie waarde, of θ.
Stel dat onze eerste (en enige) aflezing van die multimeter - vanaf nu gedefinieerd als gemeten waarde, of X - 2,0052 A aangeeft. Dan hebben we, zoals verwacht, een absolute fout:
η = X − θ
η = 2.0052 - 2.0000 = 0.0052 A
Als we η kennen, kunnen we de relatieve fout ε berekenen, die, uitgedrukt als percentage, als volgt is:
ε = (η / θ) × 100
ε = (0.0052 / 2.0000) × 100 = 0.26%
Dit getal vertegenwoordigt een dimensieloos getal (dus zonder bijbehorende eenheid) en betekent dat onze multimeter, in deze specifieke aflezing en dit geselecteerde bereik, een relatieve fout = 0,26% vertoont.
Het maken van statistieken
De enkele meting die we tot nu toe hebben gedaan op de eerste van onze multimeters vertelt ons niet veel over de algehele betrouwbaarheid van ons instrument en stelt ons niet in staat om te bepalen of deze wordt beïnvloed door systematische fouten, willekeurige fouten of beide. Dus, voor meer zinvolle inzichten nemen we de zaak serieuzer en bouwen we vier databases van metingen op.
We voeren 100 opeenvolgende metingen uit op elke multimeter, waarbij we ervoor zorgen dat de testcondities op geen van de instrumenten variëren tussen de ene meting en de volgende. Elk van de metingen genereert een Xn-waarde.
Vervolgens berekenen we het rekenkundig gemiddelde van die metingen en definiëren dat als de gemiddelde gemeten waarde µ (met n = 100, in dit geval):
µ = (X1 + X2 + X3 … + Xn) / n
Het is echter niet voldoende om µ te kennen; hoewel het ons enkele aanwijzingen geeft over de gemiddelde nauwkeurigheid, stelt het ons niet in staat om de willekeurige component van de fout te kwantificeren, waardoor we de precisie niet kunnen bepalen.
Daarom nemen we op dezelfde verkregen gegevens voor elk van de vier databases aan dat onze metingen de wet van de normale verdeling volgen en berekenen we de standaardafwijking, σ, van aflezingen X1...X100 met de volgende formule:
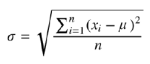
We kunnen dus controleren hoe ver de metingen afwijken van de eerder verkregen gemiddelde waarde.
Als je niet bekend bent met het begrip standaard-deviatie, kun je kijken naar of, voor een meer formele, wiskundige benadering, naar . Je kunt ook eens kijken naar De Gausverdeling, uitgelegd in het korte toegevoegde tekstblok in dit artikel.
De Gaussische verdeling in het kort
Vaak zijn in de wetenschap de belangrijkste ontdekkingen het resultaat van een combinatie van de studie van verschillende wetenschappers. Dit is het geval met de Gaussische verdeling, waarvan het concept ontstond uit verschillende observaties, te beginnen eind 1700 met de fundamentele stelling van Laplace over de centrale limiet [3], om te volgen met het inzicht van Abraham de Moivre die opmerkte dat naarmate het aantal gebeurtenissen toenam, hun verdeling een nogal afgevlakt profiel volgde, tot het werk van Carl Friedrich Gauss die de formule definieerde voor het berekenen van de curve die later zijn naam kreeg.
Een interessant historisch overzicht van deze studie, die de basis vormt van de moderne statistiek, is hier te vinden [4].
Figuur A illustreert een typische Gaussische verdelingscurve. In een normale verdeling zijn er binnen de geanalyseerde steekproef waarden die de µ-waarde - het rekenkundig gemiddelde van alle gegevens - symmetrisch benaderen met een grotere frequentie dan andere, en deze frequentie draagt bij tot de karakteristieke klokvorm van de curve.
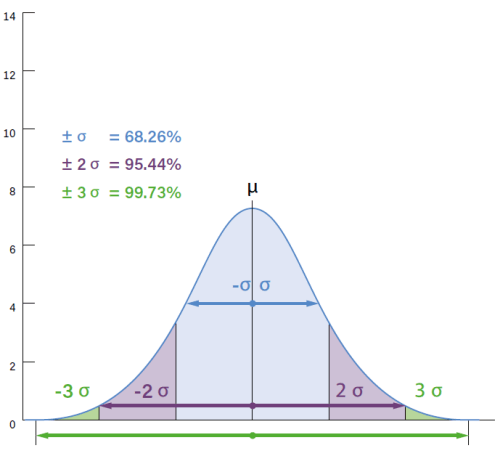
Het gebied onder de curve stelt de verdeling van de steekproefgegevens voor. De Y-as geeft aan hoe vaak gegevens met dezelfde waarde voorkomen.
De afstand tussen µ en het buigpunt van de curve (waar de kromming in de andere richting verandert) vertegenwoordigt wat gewoonlijk standaardafwijking of sigma (σ), wortel-gemiddelde afwijking of wortel-gemiddelde kwadraatfout wordt genoemd.
Met andere woorden, sigma kan worden beschouwd als een index van de spreiding van onze gegevens ten opzichte van het gemiddelde µ. Sigma en precisie zijn omgekeerd evenredig, d.w.z. als de spreiding van de gegevens afneemt, neemt de precisie toe en wordt de Gaussiaanse curve piekachtiger. Omgekeerd wordt de curve bij hoge sigmawaarden bijzonder vlak en wordt de basis breder.
Een empirische regel die vaak wordt toegepast op een standaard verdelingscurve stelt dat de steekproefgegevens een kans van 68,26% hebben om in het [-σ...σ] interval te vallen (blauwe gebied, zie figuur A), 95,44% in het [-2σ...2σ] interval (blauwe + paarse gebieden) en 99,73% in het [-3σ...3σ] (blauwe + paarse + groene gebieden).
Sigma is geen dimensieloze grootheid, maar gaat uit van de meeteenheid van de beschouwde grootheid (in het voorbeeld van onze vier multimeters is dat ampère/A).
Gegevens interpreteren
Multimeter 1
Met de honderd metingen die gedaan zijn met multimeter 1 berekenen we de respectieve gemiddelde waarde µ en standaardafwijking σ zoals hierboven vermeld. De resulterende grafiek wordt getoond in Figuur 1. De curve toont de normale verdeling van de metingen rond de gemiddelde waarde, µ, die voor dit instrument µ = 1,9 bleek te zijn. De plot van de verdeling rond µ is erg “scherp”, wat wijst op een hoge concentratie van metingen met waarden die erg dicht bij het gemiddelde liggen. Dit is echter ver verwijderd van de ware waarde θ = 2. De waarde δ = (µ - θ) = -0.1 is de uitdrukking van de gemiddelde onnauwkeurigheid van dit instrument.
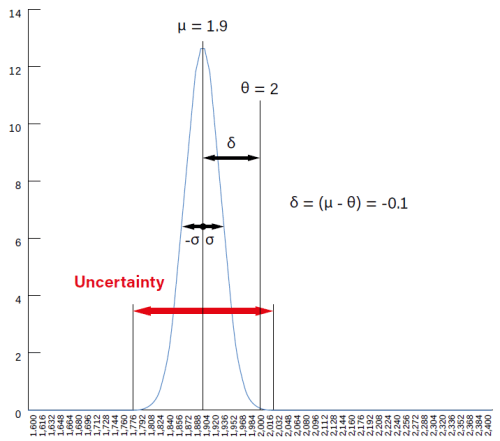
Het moet alleen gekalibreerd worden met een referentie-instrument,
omdat de δ component niet verwaarloosbaar is.
Dit is een typisch geval waarin kalibratie van het instrument kan helpen om deze foutcomponent zelfs aanzienlijk te verminderen, waardoor δ tot verwaarloosbare waarden wordt verlaagd (dicht bij 0) en de verwachte nauwkeurigheid wordt hersteld.
Het interval tussen de twee slechtste meetwaarden (de basis van de belvormige curve, aangegeven door de rode pijl) wordt ook wel de maximale meetonzekerheid genoemd. Bij metingen zijn onzekerheid en precisie omgekeerd gecorreleerd.
Met σ = 0,042 A, (d.w.z. een standaardfout van ±2,2% gemiddeld µ), kan dan geconcludeerd worden dat het instrument nauwkeurig is, maar omdat de systematische component van de fout (δ = -0,1 A) hoog is, is het niet nauwkeurig, met een gemiddelde fout = -5% ten opzichte van de referentie.
Multimeter 2
De grafiek van de tweede multimeter (Figuur 2) laat een drastisch ander scenario zien. De gemiddelde waarde µ van de meetwaarden bleek = 1,998 te zijn, maar de maximale meetonzekerheid van dit instrument is veel groter dan die van multimeter 1.

nutteloos door de aanzienlijke fout in de precisie.
Met σ = ±0,116 A (±5,8% fout gemiddeld µ) is de willekeurige component van de fout groot, met sterk verdeelde (niet geconcentreerde) meetwaarden. Omdat deze niet volledig gecorrigeerd kan worden, maakt deze willekeurige foutcomponent multimeter 2 onnauwkeurig, hoewel de schijnbaar verbazingwekkende nauwkeurigheid δ = -0,012 A (-0,6% fout op referentie) ons misschien misleidt.
Al met al een zeer nauwkeurig, maar zeer onnauwkeurig instrument dat niet in het laboratorium gebruikt kan worden, omdat de kans op het verkrijgen van onrealistische metingen groot is. Om een andere, maar veelgebruikte terminologie te gebruiken: dit instrument heeft een zeer lage herhaalbaarheid, een synoniem voor precisie.
Dit geval laat zien dat nauwkeurigheid alleen niet genoeg is voor het verkrijgen van een betrouwbare meting.
Multimeter 3
De situatie met multimeter 3 is nog slechter, als dat al mogelijk is. De grafiek van Figuur 3 geeft een berekende gemiddelde waarde µ = 2,15, met δ = 0,15 A (+7,5% fout op referentie) die op zichzelf al significant zou kunnen zijn. Bovendien, met σ = ±0.19 A (±8.8% fout op gemiddelde µ), toont de verdelingscurve een toevallige fout met een extreem afgeplatte curve. De totale onzekerheid is zo groot dat deze aan de rechterkant uit de grafiek valt. De resultaten van dit derde instrument zijn dus grofweg niet precies en onnauwkeurig..
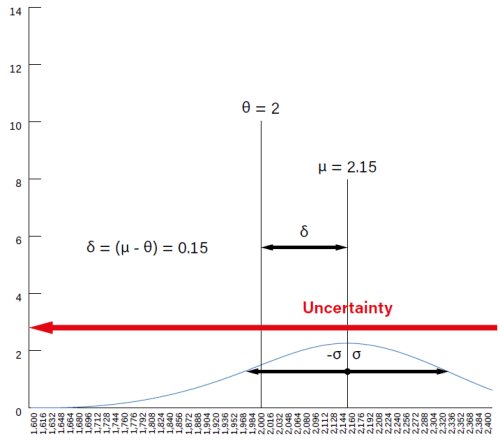
opzichte van de referentie, zo mogelijk nog verergerd door een wijd gespreide onzekerheid (zeer hoge σ).
Multimeter 4
De plot van het vierde instrument (Figuur 4) blijkt de beste van de reeks te zijn. De foutenverdeling concentreert zich op het gemiddelde van µ = 2,006, de resulterende δ = 0,006 A (+0,3% fout ten opzichte van de referentiewaarde) kan als verwaarloosbaar worden beschouwd en de waarde van de standaardafwijking σ = ±0,04 A (±2% gemiddeld µ) is laag. De conclusie die getrokken kan worden is dat dit zowel een precies als nauwkeurig instrument is, en vanwege zijn eigenschappen kan het ook gedefinieerd worden als exact.
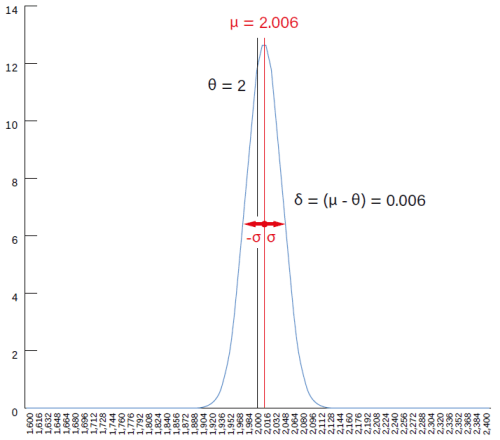
van +0,3% en ±2% op precisie is hij nog steeds nuttig op de werkbank.
A More Handy Representation
For a more practical depiction, the summary table in Figure 5 may be useful. In it, the above examples’ measurement distributions are represented on four targets. This is a widely used example in these cases, because of the very immediacy of its interpretation. In addition, the green and blue frames indicate the systematic and random error components’ areas, partially overlapping, in the worst case — multimeter 3, which is affected by high levels of both.
Ideally, the Cartesian axes could be superimposed on this drawing, where the Y axis represents precision, the X axis accuracy, and the straight line function Y = X in the first quadrant is the exactness of measurement, i.e. the combination of both.
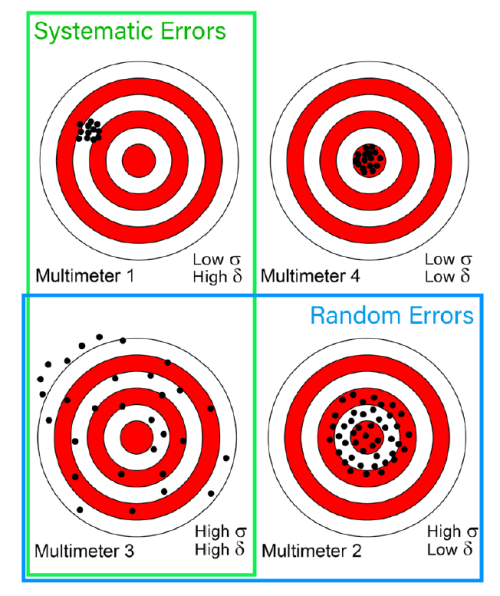
vertegenwoordigt de diameter van de geperforeerde gebieden de spreiding
(σ, de reciproke van precisie),terwijl hun afstand tot het centrum (δ) de onnauwkeurigheid aangeeft.
Multimeter 4 is niet foutloos, maar de twee foutcomponenten, systematisch en willekeurig, zijn veel lager.
Referentiewaarde of werkelijke waarde?
Aan het begin van dit artikel schreven we dat we de referentiewaarde als de werkelijke waarde beschouwden. Dit is omdat we vertrouwden op de karakteristieken van ons referentie-instrument voor het genereren van stroom, waarbij we ervan uitgingen dat het exact was voor onze standaarden.
In werkelijkheid - het spijt me dat ik je moet teleurstellen - bestaat de werkelijke waarde van elke grootheid, maar die is onbekend en ontoegankelijk, omdat elke meting onderhevig is aan een onzekerheidsniveau van meer dan 0.
Met andere woorden:
- De werkelijke waarde is perfect, maar alleen theoretisch: onmogelijk om exact te bepalen.
De referentiewaarde is de best beschikbare waarde en wordt gebruikt als (lokale) standaard bij praktische metingen.
De taak van metrologie is specifiek om de afstand tussen de werkelijke waarde en de gemeten waarde zo veel mogelijk te overbruggen.
Deze afstand wordt verkleind door verschillende standaarden te gebruiken, met een steeds hogere nauwkeurigheid, die de zogenaamde traceerbaarheids-keten van een meetinstrument vormen . Dit, en vele andere gedetailleerde aspecten van acquisitie- en afleesfouten die inherent zijn aan elektronische meetinstrumenten, zullen het onderwerp zijn van een toekomstig artikel. Blijf op de hoogte!
Noot van de redactie: Dit artikel (250046-03) verschijnt in de editie van mei/juni 2025 van ElektorMag.
Vragen of opmerkingen
Hebt u technische vragen of opmerkingen naar aanleiding van dit artikel? Stuur een e-mail naar auteur via roberto.armani@elektor.com, of naar de redactie van Elektor via redactie@elektor.com.


Discussie (2 opmerking(en))